increpare games

Introduction

Ok, I’m going to try to build some rough mathematical description of the game Jenga

You know Jenga, the game where you have a tower of little wooden blocks, and players take turns removing one block at a time from the tower, stack it on the top. The last player to stack a block without making the tower fall wins the game.

Right, well, might as well get down to it.

Row Density

Ok, on any given row there are 3 blocks. If either of the side blocks are picked, then you can remove another block (i.e., there’s a 66% chance you’ll remove two blocks), and if you pick one from the centre, then you can not remover any other blocks from the stack (i.e., there’s a 33% chance you’ll remove only one block from a given row).

Formulating this, the average no of pieces you’ll take out of any given row is:

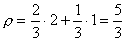
This also means that, on average, it will take 5/3 turns to exhaust any row.

So, given R rows, you will on average take 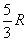turns to render the whole stack useless.

However, after each turn you will stack one block on top, so you will also have added 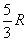pieces on top of the stack, or have created 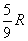new rows. With these rows, you will take 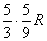turns to clear them and will generate 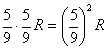extra rows, and these extra rows will generate 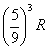, etc. etc.

So, in total, you will end up with

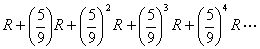
Rows by the end (note that in reality that after a certain term the terms in the sequence become less than 1, and so the above series is an overestimation).

This is a geometric series, with a=R and r=5/9, and the sum is given as:

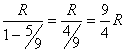
Now, each of the 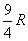rows take up roughly 5/3 turns, so the total number of turns it will take to finish up the tower is 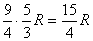turns.

Now, we know that the total number of blocks in the tower at any one time is constant, but the total number of moveable blocks in the tower reduces every turn, it goes down by one every turn, but goes up every three turns because of an extra row being added.

Thus, denoting the number of free blocks as a function of time:

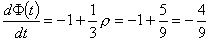
This just means that every turn the no of moveable blocks decreases by an average of 4/9. (remember that the extra row being added does not create three extra moveable pieces, it creates, 5/3 extra moveable pieces on average)

So, given that the initial number of moveable blocks is 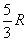, we can write

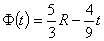
Now we can go on to some of the proper maths :)

Probability Distribution

Now, taking any area of the tower, the chance that the person will pick a block from that area is proportional to the ration of the size of that area to the size of the whole tower, or, taking that area to be a specific row in it’s initial state:

P(Will be picked)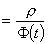

Now, let D be the average number of blocks on a given row as a function of time.

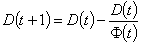
or, simplifying:

.

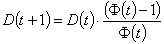Now, expanding it a little, a pattern will emerge:

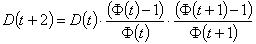
But

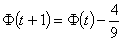
so

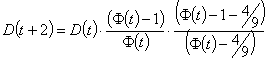
And so on…

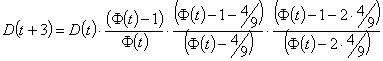
And so, by induction:

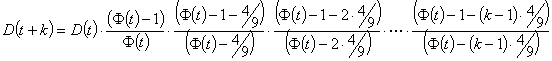
Ok, all you need to know is that the gamma function has the property that

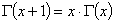
for all .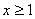

Now, lets look at part of D(t+k), namely the lower half of the D coefficient:

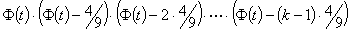
Let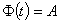

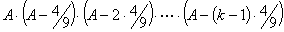
Now, look at the following:

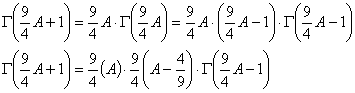
Expanding this further:

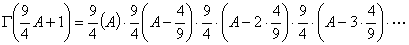
But this sequence does not end. We have to cap it be dividing by another function that will cancel out all terms after .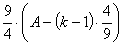

So, let’s look at the following

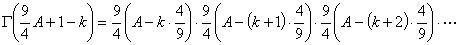
Dividing one by the other, we get

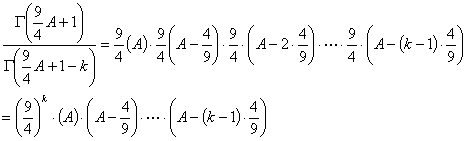
Now, we can substitute 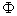for A and divide by 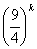to get the thing quotiented at the start of this section:

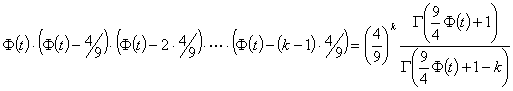
and – in addition, noting that the top half of the D coefficient from the previous section is of the same form with A as .

Back to the Distribution

So, we get the following function

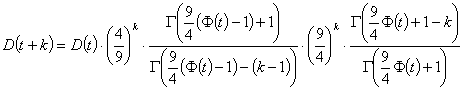
And the two fractions cancel out giving

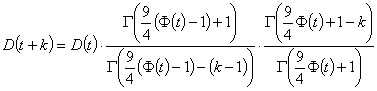
Which I think is pretty neat (coz I’ve never had a reason to use the Gamma function before, and coz gamma functions are neat :) )

Now, the rest is trivial:

Given an initial stack size of R, an additional row is created every three turns, so, rephrasing D as 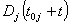where j is the row you’re looking for the number of pieces left to move, and 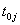is the turn on which the j^th row was created.

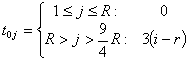
Now, the average number of blocks left to be moved on a row j can be approximated (realising that 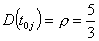) as

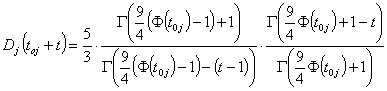
And that’s as much as I’m going to do with it. You wouldn’t believe how many weird roads I had to go down to find the above solution, and I’m sure as hell not going to go actively looking for any more geometric sequences for quite some time (I was going mad yesterday trapped in a maze of them!).

Hope it made some sense, will clarify anything if you feel that anything’s badly explained.