A prelude
It took me a long long time to cop on to what the deal was with resolutions. But, I was, a bit ago, walking somewhere, and I saw something, or thought of something (I can’t remember what), and was like “oh, that’s just like a projective resolution”. I also had a dream about the Hilbert Syzygy theorem a few weeks ago. Can’t remember the details of that either, surely they were fascinating, though. I should probably take more descriptive notes. Ho hum… .
A difference in usage
Here’s a simple word which has markedly different connotations to mathematicians and non-mathematicians (in that the technical sense of the word can be, roughly, applied to the same situations as the non-technical one).
If you, as a nonmathematics-exposed person, say that Anne tends to project her misery onto everyone else, you would probably mean that she goes around believing everyone else to be exactly as miserable as she is.
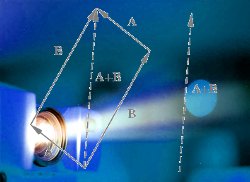
However, to a mathematician, projection has a different intuitive feeling – projecting A onto B connotes the action of “picking out” what elements of A are common to B. That is, if you said to me that Anne tends to project her misery onto everyone else, I would be likely to feel that she only sees in other people is misery – and not only any misery, but a misery that resonantes with her own, if any. So, if I project my happiness onto you as a mathematician, I see in you what aspects of your happiness are similar to mine.
(this came out of a chat with greg).
A geometric fantasy
I was walking down the street about two weeks ago, and I thought “what if I think about myself as living in projective space?”. And I tried. Projective space is a “compactification” of our normal “affine” space, and corresponds to adding some points and calling them “infinity” (in some strikingly pleasant way), without really changing much of their local structure. But the thing is it turns spaces infinite in extent, like our “affine” space, and turns them into objects that are finite in extent (it turns the infinite line into a circle, for example). But yes, it made things feel different. The sky was no longer so far away, and everything felt as if brightly illuminated and indoors – intimate, being an appropriate word, perhaps.
2 Comments
Not sure that I follow this (i.e., the business of projections ‘picking out’ things.
Time to indulge in a spot of pedantry?
The words ‘project’ and ‘projection’ come from the past participle of the Latin verb
proicio, proicere, proieci, proiectum
which (according to my dictionary) means “to throw down, fling forwards, to banish”. It comes from combining the prefix ‘pro’
(in front of, on behalf of, etc.) with the verb
iacio, iacere, ieci, iactum
which means “to throw, to build” (this last meaning of ‘iacio’ obviously giving rise to ‘projections’ on buildings).
It is surely true to say that the word ‘projection’ came into mathematics in the context of geometry, and geometrical optics in particular. Think of a light source projecting an image onto a screen, or onto the retina of the eye. I at any rate have a mental picture of that image being thrown forward onto the screen.
And of course ‘projective geometry’ originated in the study of perspective, and deals with those properties of geometric figures (such as incidence relations, cross ratios etc.) that remain invariant under such projections. Think of a setting up a slide show at home (assuming people still have collections of transparencies), where you have to fiddle around with the orientation of the screen in order to get a rectangular picture. The properties of the picture that remain the same as you wiggle the screen around are projective invariants.
So this naturally gives rise to the idea of ‘projecting’, say, a curve in space onto a two-dimensional plane, with a corresponding mental image of taking that curve and squashing it flat onto the plane.
So one has the notion of projecting three-dimensional space (and geometrical figures in three-dimensional space) onto two-dimensional and one-dimensional subspaces.
It is a natural extension to talk about the ‘projection function’ that maps a Cartesian product of sets onto one of its factors.
And, by extension, one tends to apply the term ‘projection’ to surjective functions which behave in a similar fashion, such as covering maps and the projection maps associated with fibre bundles. I certainly have a mental image of a covering map squashing the covering space flat onto the base space, or throwing points of the covering space down onto the base space. Similarly with fibre bundles.
And one would imagine that the Bourbaki mathematicians who came up with terms like ‘injective’ and ‘surjective’ functions thought in terms of functions as throwing elements from one set to another, or perhaps throwing one set into or onto another.
And, of course, when you ‘reject’ something, you throw it back.
And before we leave the subject of Latin origins of some English words, it is curious to note that the verbs ‘transfer’ and ‘translate’ originate in the same Latin verb, which must be one of the most irregular in the language:
fero – I bear, I carry
ferre – to bear, to carry
tuli – I bore, I carried
latum – borne, carried
If you add the prefix ‘trans’ (across) you get ‘transfero’ etc.,
which has the following meanings listed in my Latin dictionary:
to bring across, to transport, to transfer, to translate, to copy.
e.g. coordinate functions on vector spaces pick out certain coordinates, symmetrization/anti-symmetrization operations on tensor-spaces pick out various symmetric/antisymmetric parts of tensors, the projection on bundles picks out base points (and if one thinks of it mapping a bundle onto the trivial bundle, one has that applying it twice gives the identity).
I can’t respond too much to the later stuff, but yes, I had never thought of the words that way – it’s a nice way to think about them, would probably have made remembering them in first year a lot easier had I bothered to look up what the words mean :)